Density Altitude Calculator
The Importance of Density Altitude in Aviation
Our atmosphere is a dynamic system with variations in pressure, temperature, humidity and precipitation typically seen throughout the day across a relatively small area. These changes in the local environmental conditions cause associated changes to the air density, which plays a crucial role in determining aircraft performance.
Air Density and Aircraft Performance
An increase in the air density is associated with an improvement in both the aerodynamic performance and the thrust generated by an aircraft. Conversly, a reduction in the air density results in less engine power being produced, and less lift generated by the wings, which will result in a loss in performance at critical phases in flight such as takeoff.
- A drop in air density results in less lift being produced by a wing at a given airspeed and angle of attack.
- A drop in air density results in a loss in power generated by the engine (especially true in normally aspirated general aviation aircraft engines).
- Propeller driven aircraft will see an additional loss in thrust due to a drop in air density as a result of the propeller being unable to extract as much thrust at a given RPM (a propeller acts in the same way as a wing with an airfoil section designed to generate a force due to the pressure variation over the upper and lower surfaces).
Losses in aircraft performance are most noticable during takeoff and climb out at high altitudes, and on hot days.
Factors Affecting Air Density
Air density is driven by three primary factors. These are altitude, local pressure variations, and local temperature variations. Humidity also has an effect on the air density but to a lesser extent.
- Altitude: An increase in altitude results in a decrease in air density with a corresponding drop in static pressure and temperature.
- Local pressure variations: regions of high and low pressure associated with local weather phenomena result in density variations. Higher pressures result in more dense air and lower pressures less dense air.
- Local temperature variations: higher temperatures are associated with lower air density, and cooler temperatures with higher air density.
The Standard Atmosphere Model
The atmosphere is in a constant state of flux due to global and local weather phenomena. Since local conditions vary at all places and at all times aeronautical engineers work with a theoretical atmosphere model when performing aircraft performance analysis calculations such as those that appear in aircraft Pilot Operating Handbooks. This atmosphere model is referred to as the International Standard Atmosphere and provides a mathematical model describing how pressure, temperauture, density and viscosity vary over a range of altitudes from sea level to 80 km.
The AeroToolbox Standard Atmosphere Calculator has proven to be a popular tool which outputs the relevant atmospheric properties given an altitude and temperature or temperature offset from standard.
Sea level standard conditions are very important from an aviation stand point as airspeed indicators are calibrated on the assumption that the aircraft is operating at sea level on a standard day.
| Temperature | 15 °C |
| Pressure | 1013.25 hPa |
| Density | 1.225 kg/m³ |
Of course there are very few instances when an aircraft is actually operating in these standard conditions, and as such the true airspeed will usually differ from the indicated airspeed — oftentimes by a substantial amount. You can play around with our Airspeed Conversion Tool to see this in action. The tool is especially useful when wanting to calculate true airspeed given indicated airspeed and an operating altitude.
Performance Charts
To show the importance of the prevailing atmospheric conditions on aircraft performance you only need to open any aircraft POH to the section dedicated to takeoff performance. The example below is from a Piper PA-28-121 Archer II manual and plots the variation in takeoff performance with pressure altitude and operating air temperature at a flaps 25 setting. The pressure altitude corrected for the operating air temperature is of course the density altitude.
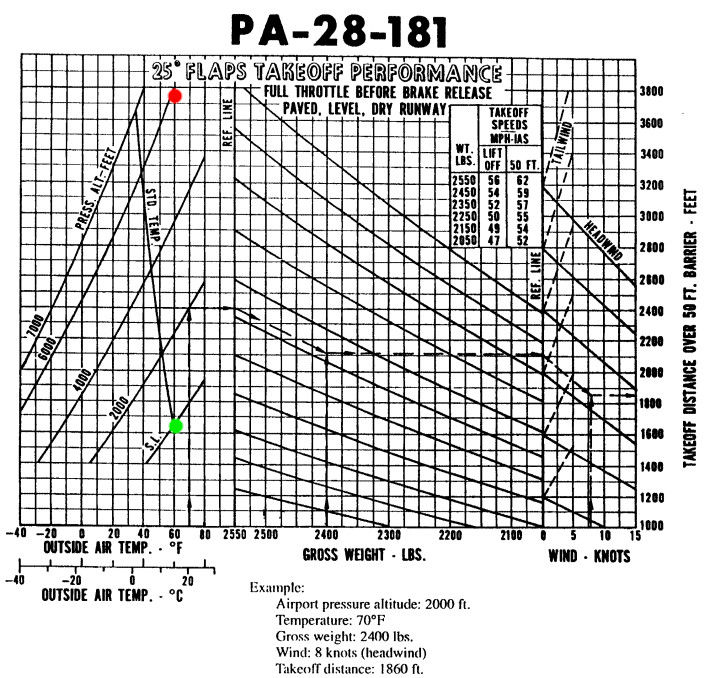
- On a hot day with pressure altitude of 6000 ft, the gross weight takeoff run in windless conditions is approximately 3700 ft.
- A standard day at sea level (15°C) at gross weight in windless conditions results in a takeoff run closer to 1600 ft. This is less that half of the hot and high takeoff run!
This is a great example of the effect that density altitude has on performance. An airport at 5000 ft elevation with an outside air temperature of 32°C has a density altitude in excess of 8000 ft. This is why it is so important to know and understand your aircraft and it's performance limitations before embarking on a flight — especially at or near gross weight on a hot day at higher altitudes.
AeroToolbox Calculation Methodology
The published calculator at the top of the page uses a dry air approximation. To calculate the density altitude you first need to determine the pressure altitude. This is the altitude in the standard atmosphere model that has the same atmospheric pressure as the current atmospheric pressure in the region of interest (usually an airfield).
The pressure altitude is then corrected by the difference in temperature between the standard temperature at the calculated pressure altitude and the actual outside air temperature. This correction yields the density altitude.
Pressure Altitude
The pressure altitude \( \left( \textnormal{PA} \right) \) is determined from the airfield elevation and the local QNH using a formula published by the National Oceanic and Atmospheric Administration (NOAA).
The altitude output is in feet and the QNH value must be converted to milibar (mb) before being used in the equation.
$$ \textnormal{PA} = \textnormal{Field Elevation} + 145366.45 \left[ 1 - \left(\frac{\textnormal{QNH}_{mb}}{1013.25}\right)^{0.190284} \right]$$
To convert QHN from inches of mercury to milibar:
$$ \textnormal{QNH}_{mb} = \textnormal{QNH}_{inHg} \times 33.86388 $$
QNH is often given in hectopascal (hPa) which is the same an millibar.
$$ \textnormal{QNH}_{mb} = \textnormal{QNH}_{hPa} $$
Density Altitude
To calculate the density altitude you first need to estimate the current atmospheric pressure at the airfield. This is done by converting the pressure altitude calculated above to a static pressure using the standard atmospheric model.
The equations that follow all use the same set of constants which are added to the table below for easy reference.
| Symbol | Value | Units | Description |
|---|---|---|---|
| \( g \) | 9.80665 | m.s² | Acceleration due to gravity |
| \( M \) | 0.028964 | kg/mol | Molar mass of dry air |
| \( R \) | 8.31432 | J/mol K | Universal Gas Constant |
| \( \Gamma \) | 0.0065 | K/m | Environmental Lapse Rate (valid below 11 000 m) |
| \( T_{0} \) | 288.15 | K | Sea level Standard Temperature |
| \( P_{0} \) | 101325 | Pa | Sea level Standard Pressure |
Relative Pressure
The relative pressure term \( \sigma \) refers to the ratio of the atmospheric static pressure at a given altitude to that in sea level standard (ISA) conditions. The temperature should be converted to Kelvin for all proceeding calculations.
$$ \sigma = \left( \frac{T_{0}}{T_{i}} \right)^{\frac{-gM}{R \Gamma}} $$
Where:
\( T_{i} \) is the standard temperature at the pressure altitude.
\( T_{0} \) is the standard temperature at sea level ISA conditions (288.15 K or 15°C)
The standard temperature at the pressure altitude can be determined from the previously calculated pressure altitude (converted to metres) and the environmental lapse rate \( \Gamma \).
$$ T_{i} = T_{0} - \left( \Gamma \times \textnormal{PA}_{m} \right) $$
Once the relative pressure \( \sigma \) is known then the static pressure corresponding to the pressure altitude follows.
$$ P_{PA} = \sigma \times P_{0} $$
Where:
\( P_{PA} \) is the static pressure corresponding to the previously calculated pressure alltitude (function of QNH).
\( P_{0} \) is the standard atmospheric pressure at sea level under ISA conditions (101325 Pa).
Density Altitude
The density altitude is then determined using the ratios of the pressures and temperatures between the actual atmospheric conditions and that of the standard atmosphere model at sea level.
$$ \textnormal{DA} = \frac{T_{0}}{\Gamma} \left[1 - \left( \frac{P_{PA} / P_{0}}{T / T_{0}} \right)^{\frac{\Gamma R}{gM-\Gamma R}} \right] $$
Where:
\( P_{PA} \) is the pressure corresponding to the previously calculated pressure alltitude (function of QNH).
\( P_{0} \) is the standard atmospheric pressure at sea level under ISA conditions (101325 Pa).
\( T_{0} \) is the standard temperature at sea level ISA conditions (288.15 K).
\( T \) is the outside air temperature at the airfield (K).
Density Altitude Approximation Formulae
A common approximation method for calculating the density altitude is presented below. These equations are generally used by pilots before getting airborne on hot days at or near gross weight. We would suggest rather bookmarking this page and making use of our calculator, but the density altitude calculation as presented here is often used as an exam question during the theory portion of the PPL.
Pressure Altitude Approximation
To convert from airfield elevation to a pressure altitude when the current QNH is known:
$$ \textnormal{PA}_{hPa} \approx \left( 1013.25 - QNH_{hPa} \right) \times 30 ft + \textnormal{field elevation} $$
If the QNH is given in inches of mercury:
$$ \textnormal{PA}_{inHg} \approx \left( 29.92 - QNH_{inHg} \right) \times 1000 ft + \textnormal{field elevation} $$
If you are sitting in your aircraft then the pressure altitude can be quickly determined by setting your altimeter to 1013.25 mb or 29.92 inHg and reading off the resulting altitude.
Density Altitude Approximation
The density altitude can be estimated using the pressure altitude as an input and the simple formula below.
$$ \textnormal{DA} \approx \textnormal{PA} + 120 \left ( T - T_{ISA} \right) $$
Where:
\( T \) is the current Outside Air Temperature in °C.
\( T_{ISA} \) is the standard temperature at the given airport elevation in °C.
The variation in standard temperature with altitude can be approximated between sea level and 36 000 ft by the following equation:
$$ T_{ISA} \approx 15 - \left( 0.00198 \times \textnormal{PA} \right) $$
Approximation Worked Example
Calculate the pressure and density altitude given the following conditions:
\( \textnormal{Airfield Elevation} = 5000 \textnormal{ ft}, \)
\( \textnormal{QNH} = 1018 \textnormal{ hPa}, \)
\( \textnormal{OAT} = 30 ^{\circ}C \)
First approximate the pressure altitude:
$$ \textnormal{PA}_{hPa} \approx \left( 1013.25 - 1018 \right) \times 30 + 5000 = 4858 \textnormal{ ft} $$
Then calculate the temperature deviation from standard:
$$ T_{ISA} \approx 15 - \left(0.00198 \times 4858 \right) = 5.38 ^{\circ}C $$
The approximate density altitude follows:
$$ \textnormal{DA} \approx 4858 + 120 \left (15T - 5.38 \right) = 7812 \textnormal{ ft} $$
Comparison with Calculator
These results compare well to the more accurate analysis performed in the calculator at the top of the page.
| AeroToolbox Calculator | Approximation Formulae | % Difference | |
|---|---|---|---|
| Pressure Altitude (ft) | 4871 | 4858 | 0.3 |
| Density Altitude (ft) | 7644 | 7812 | -2.1 |
Popular Posts
