Crosswind Calculator Methodology

The most reliable and efficient way to calculate the head/tail wind and crosswind component of the wind relative to the runway heading is to make use of vector notation and the concept of the scalar dot product.

Let’s go through how to perform the calculation.

Vector and Scalar Notation

Vector and Scalar quantities are mathematical formulations that assist us in modelling the physical quantities of the world around us. There is a separate post on AeroToolbox.com where the differences between vector and scalar quantities are described in more detail; but for the purposes of this calculation, it is enough to say that the essential difference between a scalar and vector quantity is that:

• A vector quantity is such a quantity that requires both a magnitude and a direction to fully describe it.
• A scalar quantity is a quantity that can be fully described by a magnitude only.

Temperature is a good example of a scalar quantity – it would be meaningless to try and describe the outside air temperature in terms of some direction.

Wind speed (or more correctly the wind velocity) can only be fully described when quoting the wind speed (magnitude) and the prevailing wind direction. This is especially true when it comes to aeronautics; as the wind direction is crucial to everything from selecting the correct runway from which to take-off or land, to flight planning and fuel management.

A runway can also be described in terms of vector notation as any runway has a length (magnitude) and a magnetic heading (direction).

The problem of calculating the components of the prevailing wind relative to the runway heading therefore can be solved by representing the wind and the runway as two vectors and finding the angle between them. This is conveniently achieved using the scaler dot product.

Scalar Dot Product

The dot product of two vectors A and B is written \(A \cdot B\) (read as A dot B) and is interpreted as the magnitude of vector A multiplied by the magnitude of the component of B in the direction of A. The result is a scalar and is illustrated below.

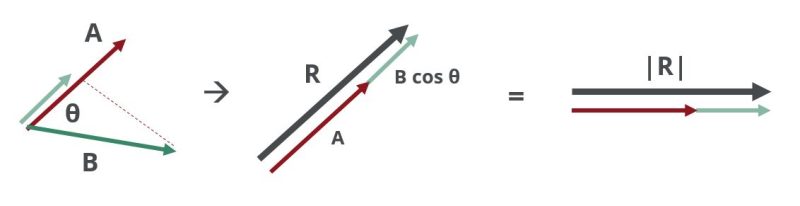
Written Mathematically:

$$ A \cdot B = |A||B|\cos{\theta} $$

Where the straight brackets |A| represents the magnitude of the vectors (the wind speed in our case). The answer is a scalar quantity represented in the image above by |R|.

The wind and the runway are both vector quantities (have a magnitude and direction) and so the dot product of the two will give us \( \theta \) which is the angle between them. We can therefore rearrange the equation and solve for the angle between the runway and the prevailing wind.

$$ \cos{\theta} = \frac{A \cdot B}{|A||B|} $$

Once we have the angle between the wind and the runway, we can easily resolve this into a parallel component (headwind or tailwind) and a perpendicular component (crosswind from the left or right) using trigonometry.

What makes the dot product so powerful is that it will correctly output the wind components for any combination of runway heading and wind vector, regardless of whether the angle between them is acute or obtuse.

Calculating the Dot Product

Given two vectors A and B, the dot product between them is calculated as:

$$ A \cdot B = \left( A_{x} \cdot B_{x} \right) + \left( A_{y} \cdot B_{y} \right) = |A||B|\cos{\theta} $$

The subscripts refer to the components of the vectors in the x and y direction.

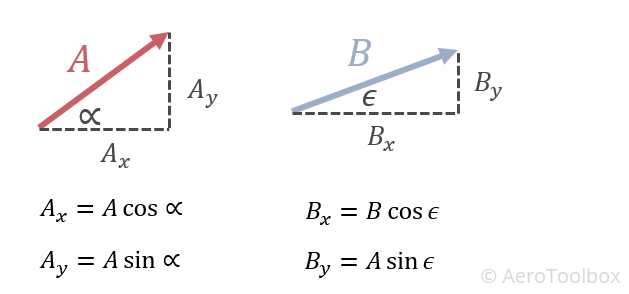
The dot product is calculated by multiplying the x-components of the two vectors and adding this to the product of the y-components. The result is a scalar which means you will simply end up with a number after calculating the dot product.

The angle between the two vectors follows once the equation is rearranged to solve for the angle theta.

$$ \cos{\theta} = \frac{A \cdot B}{|A||B|} $$

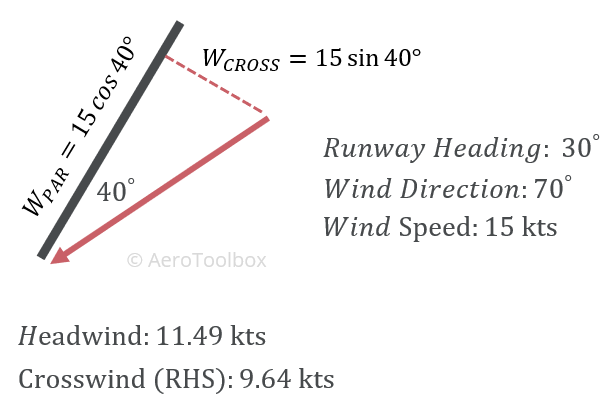
Worked Example

Let’s work through an example now and show how the dot product can be used to calculate the parallel and crosswind components.

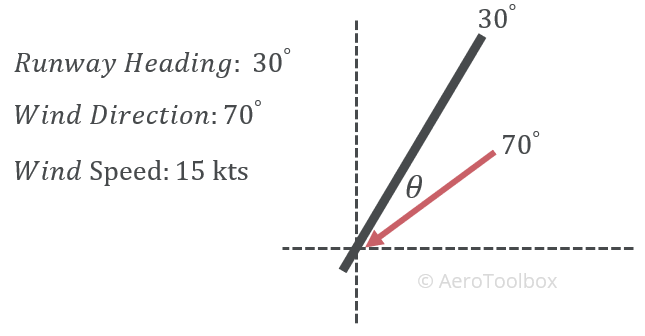
We’ll first work out the angle between the runway and the wind using the dot product, and then the magnitude of two wind components. Since we are only interested in the angle between the two, we can assume that the length of the runway and wind vector are equal to one to simplify the calculation. Also remember to convert the degree angles of the runway and wind vector to radians if you are performing the calculation in a spreadsheet.

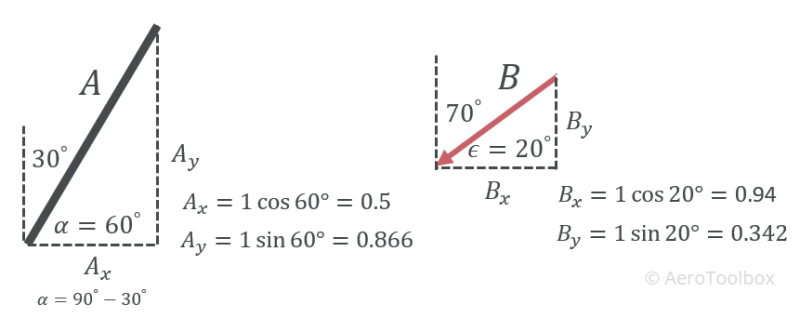
$$ A \cdot B = \left( A_{x} \cdot B_{x} \right) + \left( A_{y} \cdot B_{y} \right) = 0.766044 $$

$$ \cos{\theta} = \frac{A \cdot B}{|A||B|} = \frac{0.766044}{1} = 0.766044 $$

$$ \theta = 0.6981317 \ rad = 40° $$

Now we work out the two components of the wind relative to the runway using trigonometry and the definition of a right angle triangle.

Wrapping Up

The dot product may seem like overkill in the example above where the angle between the runway and the prevailing wind is simple to calculate. However, the dot product makes it easy to quickly determine whether the component parallel to the runway is a head or tail wind.

If you repeat the example above but use the reciprocal runway (210°), your parallel component result will be negative which indicates a tailwind.